72法则的定义与由来
72法则是一种基于复利原理的金融计算法则,用于快速估算在特定年回报率下,投资本金翻倍所需的时间。说白了,其实就是计算投资本金翻倍所需时间的一个公式。
使用法则的前提就是假设我们所有的投资回报率和分红,都是会重新投放进本金融,继续用来投资的。
➢法则计算公式

•即用72÷年回报率,得到的数字就是需要多少年能够实现资金翻倍
例如:
用年回报率为8%的投资工具,经过72÷8得到的结果是9年的时间,本金就能翻一倍。利用12%的年回报率的投资工具,则需要72÷12.6年的时间实现本金翻倍。
就相当于需要找到一种投资回报率能够达到9%和6%的理财工具,就能实现目标。
➢法则的由来
相比复利表的局限性,72法则将计算简化为数学公式,使投资者更灵活评估增长速度。也就是说我们把定期复利的将来值设为FV,现在值为PV,t为投资期数,r为每一期的利率。
计算FV的公式:
•定期复利的将来值=现在值×(1+每一期的利率)的t次幂
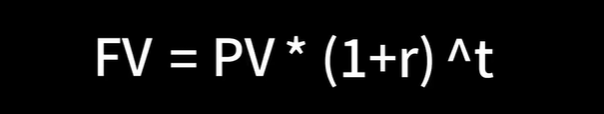
因为我们的目的是让本金翻倍,也就是说定期复利的将来值是现在值的两倍,即FV等于2PV。上面的公式即可简化为2=(1+r)^t。
具体这个方程怎么解并不重要,我们只要知道最终的结果就是t≈(0.693147÷r)再除以一个百分号,就得到了69.3147表示在低利率情况下,本金翻倍所需的时间可以由此估算。
那么可能有朋友会问,这撑死了也是69.3法则,和72还差这一点呢。是为了简化计算,因为72有更多因数(1. 2. 3. 4. 6. 8. 9. 12)便于整除,计算的时候更为方便。
72法则的适用范围与调整方法
➢法则的前提条件
•年回报率必须固定(例如,每年固定8%)。
•适用于常见投资回报率区间(4%-15%),但需根据具体回报率调整计算方法。
➢法则的局限性
•在6%到10%的年回报率范围内,计算结果比较准确。
•当回报率高于10%或低于6%时,准确度会下降。
| 年回报率 | 适用计算方法 | 计算公式 |
| 6% - 10% | 直接使用72法则 | 72 ÷ R |
| 高于10% | 增加1(每增加3%) | (72 + 1) ÷ R |
| 低于6% | 使用69.3法则 | 69.3 ÷ R |
➢法则的调整方法
•以8%的投资回报率作为中间值。
•每增加3个百分点,使用72+1。
•每减少3个百分点,使用72-1。
•对于高回报率,被除数越大,结果越准确。
•对于低回报率,使用69.3法则更为准确。
| 年回报率 | 计算方法 | 计算结果(翻倍所需时间) |
| 5% | 69.3 ÷ 5 | 13.8年(更准确) |
| 6% | 72 ÷ 6 | 12年 |
| 8% | 72 ÷ 8 | 9年(基准) |
| 11% | (72+1) ÷ 11 = 73 ÷ 11 | 6.6年 |
我们来通过举例对比一下同一回报率下的计算误差:
| 计算方法 | 计算公式 | 结果 |
| 72法则 | 72 ÷ 5 | 14.4年 |
| 69.3法则 | 69.3 ÷ 5 | 13.8年 |
| 误差:约0.6年(半年) | ||
总结:
标准72法则 适用于 6%-10% 的回报率。
高于10%时,增加1调整,低于6%时,使用69.3法则。
这项法则简单实用,但要考虑回报率的变化,以减少误差。








