凯利公式是什么?
凯利公式(Kelly Criterion)是一种用于确定理想下注金额的公式,目的是在正期望值的赌局中最大化长期增长率。它常被用在股市中,帮助长期投资者或投机者增加股票操作的绩效。
它最初由贝尔实验室的工程师约翰·凯利(John Kelly)提出,用于解决电话信号传输中的噪声问题。后来,他的同事发现这个公式可以应用于赌博,从而在赌场上大赚一笔。随后,投资者也开始使用这个公式来指导投资决策。
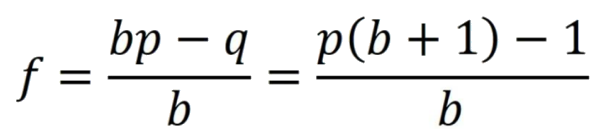
公式的基本形式如下:
f∗=(bp−q)÷b
其中:
f*:每次投资的最佳仓位比例。
b:每次获胜时的赔率(即获利比例)。
p:获胜的概率。
q:失败的概率,q=1−p。
凯利公式在投资中的计算方法
公式的核心在于通过计算期望值(优势)和赔率,确定每次投资的最佳仓位比例。以下是两个具体的计算示例:
示例1:高赔率投资机会
假设某投资机会的赔率为50%(即赚一倍),胜率为60%。计算过程如下:
| 项目 | 内容 | 计算公式 | 结果 |
| 赢的期望值 | 上升空间 × 上升几率 | 50%×60% | 30% |
| 输的期望值 | 下跌空间 × 下跌几率 | −30%×40% | -12% |
| 期望值(优势) | 赢的期望值 - 输的期望值 | 30%−12% | 18% |
| 代入凯利公式 | f∗=bbp−q | 50%18% | 36% |
| 结论 | 每次下注的仓位 | 36% |
结论:在这种情况下,每次投资的仓位应为本金的 36%。
示例2:低赔率但高胜率投资机会
假设某投资机会的赔率为20%(即赚20%),上升空间为20%,下跌空间为10%,上升几率为80%,下跌几率为20%。计算过程如下:
| 项目 | 内容 | 计算公式 | 结果 |
| 赢的期望值 | 上升空间 × 上升几率 | 20%×80% | 16% |
| 输的期望值 | 下跌空间 × 下跌几率 | −10%×20% | -2% |
| 期望值(优势) | 赢的期望值 - 输的期望值 | 16%−2% | 14% |
| 代入公式 | f∗=(bp−q)÷b | 14%÷20% | 70% |
| 结论 | 每次下注的仓位 | 70% |
结论:在这种情况下,每次投资的仓位可以达到本金的 70%。
凯利公式在投资中的核心原则
赢面大小决定仓位:
赢面大时,可以适当增加仓位,即下注较大比例的本金。
赢面小时,应减少仓位,避免因过度投入导致的风险。
仓位随本金调整:
随着本金的增减,仓位比例应动态调整,确保风险始终可控,避免因过度投入而导致资本的剧烈波动。
变量的主观性:
公式中的变量(如上涨空间、下跌空间、胜率等)在股市中往往较为主观,难以精确估计。
投资者需要结合自身的市场分析能力、经验及合理的预估来应用公式。
非必胜法则:
凯利公式不能保证100%成功,只是一个操作准则,而非精准操作方法。
投资者不应期望通过公式实现绝对的致富。
长期思维:
股市操作应注重长期大赚小赔,关注整体输赢几率,而非单笔交易的输赢。
长期累积的收益才是投资成功的关键。
选择赢面大的股票:
投资者应选择具有较大胜率和盈利潜力的股票进行投资,避免过度投注在不确定性较大的股票上。
通过基本面分析、技术分析等手段,挑选优质标的。
持续且规律的操作:
投资者应持续、规律地进行操作,根据市场情况和胜率调整每次投资金额的比例。
避免情绪化决策和盲目跟风,保持理性和计划性。
设定盈利和止损点:
在每次投资前设定明确的盈利目标和止损点,确保风险得到有效控制。
盈利时及时锁定收益,亏损时果断止损,避免损失扩大。
总结
凯利公式为投资者提供了一种科学合理的仓位管理工具,帮助在投资中优化策略,提高胜率并控制风险。投资者需结合实际情况灵活运用,注重长期思维和风险控制,从而实现稳健的长期。