損益表是什麼？

損益表記錄的是公司在一個期間內的經營成果，它從營業收入開始，一路扣除各項成本與費用，最後得出淨利。又被稱爲利潤表，是衡量公司盈利能力的直接體現，它記錄了公司在特定期間內的收入(Revenue)、成本(Costs)和利潤(Profit)。

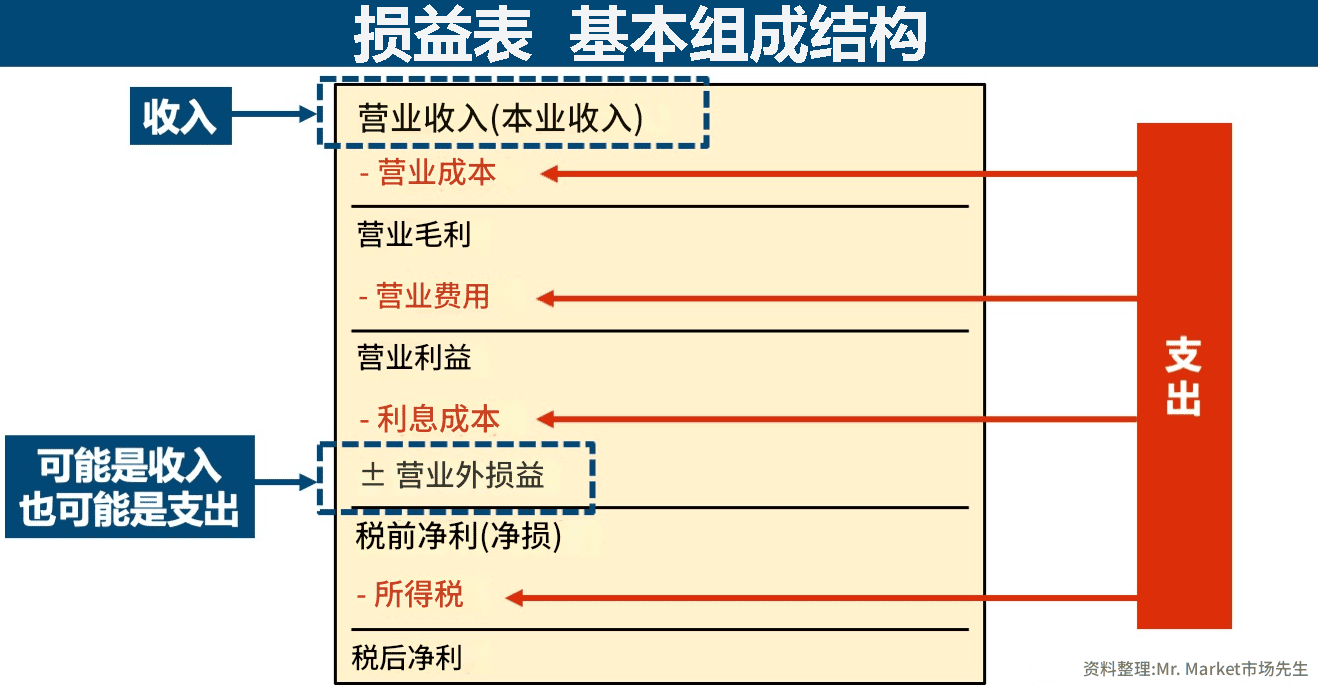損益表的基本組成結構我們來拆解它的組成結構：

1. 營業收入（Revenue）：公司通過銷售產品或提供服務獲得的總收入。

2. 營業成本（Cost of Goods Sold, COGS）：直接與生產或銷售商品相關的成本。

3. 毛利（Gross Profit）：營業收入減去營業成本後的餘額，反映了銷售商品的直接盈利能力。

4. 營業費用（Operating Expenses）：包括管理費用、銷售費用、研發費用等，這些費用不直接參與產品生產，但對企業的日常運營至關重要。

5. 營業利潤（Operating Profit）：毛利減去營業費用後的餘額，反映了公司主營業務的盈利能力，是衡量營運效率的關鍵指標。

6. 非經常性損益（Non-recurring Income/Expense）：如資產出售收益、一次性費用等，這些通常不反映公司的核心業務能力。

7.稅前利潤（Pre-tax Profit）：營業利潤加上非經常性損益後的餘額。

8.淨利潤（Net Profit）：稅前利潤減去所得稅後的餘額，即公司在一定時期內的最終盈利。

舉例說明：假設有一家名爲科技公司，其年度損益表如下：

損益表實際示例

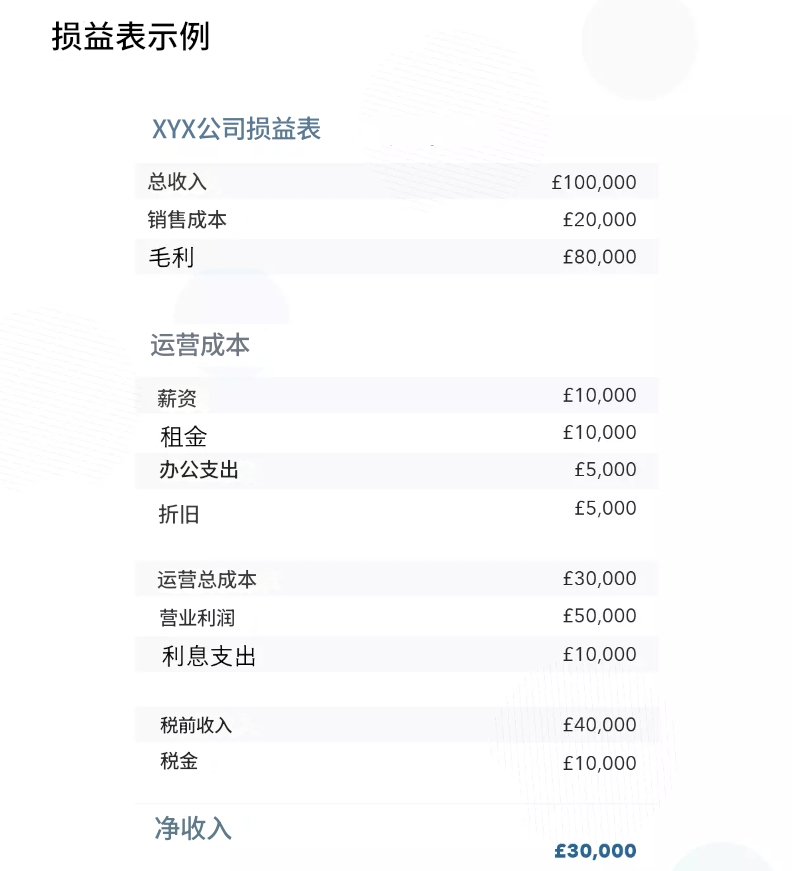
其計算過程如下：

  • 總收入: £100000

  • 銷售成本: £20000 → 毛利: £80000

  • 運營成本: £30000 (薪資£10000 + 租金£10000 + 辦公£5000 + 折舊£5000)

  • 營業利潤: £50000 (毛利£80.000 - 運營成本£30000)

  • 利息支出: £10000 → 稅前收入: £40000

  • 稅金: £10000 → 淨收入: £30000

通過這個損益表，可以清楚地看到該公司如何從收入中扣除成本和各項費用，最終實現了3萬英鎊的淨利。

要知道，如果一家公司長期無法實現盈利，其長期經營能力將受到質疑，這與個人的收支平衡道理相同——如果支出持續超過收入，最終將難以爲繼。

損益表如何判斷投資潛力？

通過損益表，投資者可以清晰地看到公司是否賺錢，以及賺錢的來源和方式。不僅告訴我們公司“有沒有賺錢”，更能揭示“怎麼賺錢”。同時，它還能幫助投資者預測未來的投資潛力。

舉例說明：假設有家咖啡店的損益表如下：

項目 金額（元）
收入 500000
銷貨成本 100000
毛利 400000
營運成本 200000
稅前利潤 200000
稅款 56000
稅後淨利 144000

說明：這間咖啡店一年賺了 14.4 萬元，如果我們考慮投資：

投資判斷1：是否值得花100萬收購?

這時我們可以計算投資回報率（年報酬率）：

  • 投入 100 萬，一年賺 14.4 萬 → 回報率 14.4%

聽起來還不錯，但我們不能只看這一年：

  • 若這家店過去幾年都只賺 1 萬，今年突然賺 14.4 萬，可能只是偶發現象，未來不一定持續。

  • 若過去 10 年平均每年都賺 14～16 萬，且有成長趨勢，這間店可能就很有投資價值。

投資判斷2：股票是否值得投資？

若這家公司有 10 萬股在外流通，每股的淨利就是：

每股盈餘（EPS） = 淨利 / 總股數 = 16 萬 / 10 萬 = 每股賺 1.6 元

這個 EPS 就是投資者最關心的數據之一。接着我們可以對照股價，計算本益比（PE ratio）來判斷是否值得買入。

損益表中的陷阱與重點

在分析損益表時，有幾個要特別留意的地方：

1. Other Income / 一次性收入

如果某季“Other Income”數額特別大，可能是公司出售資產、匯兌收益等，這些屬於一次性收入，不具持續性，因此不能當作公司穩定盈利的依據。

舉例：某公司該季度營收爲 5800 萬，但 other income 達 8246 萬，顯然這不是本業賺錢，而是靠資產處理，這種盈利模式並不可靠。

2. 縱向與橫向比較：YOY 與 QOQ

  • YOY（Year over Year）：與去年同期相比，是否進步？

  • QOQ（Quarter over Quarter）：與上季度相比，有無成長？

兩個指標都有助於評估公司經營趨勢與成長能力。

損益表還有哪些重要數據？

  • EPS（每股盈餘）：衡量股東收益，是決定股價的重要基礎。

  • Net Margin（淨利率）：公司最終的獲利能力。

  • Operating Margin（營業利益率）：公司本業的經營效率。

  • Gross Margin（毛利率）：產品本身附加價值的衡量。

總結：

損益表不僅僅是“賺或虧”這麼簡單，而是一張全面揭露公司賺錢邏輯的地圖。透過它我們可以：

  • 判斷公司營運是否健康

  • 分析收入結構與成本效率

  • 評估未來投資價值與風險