标准差

标准差的定义

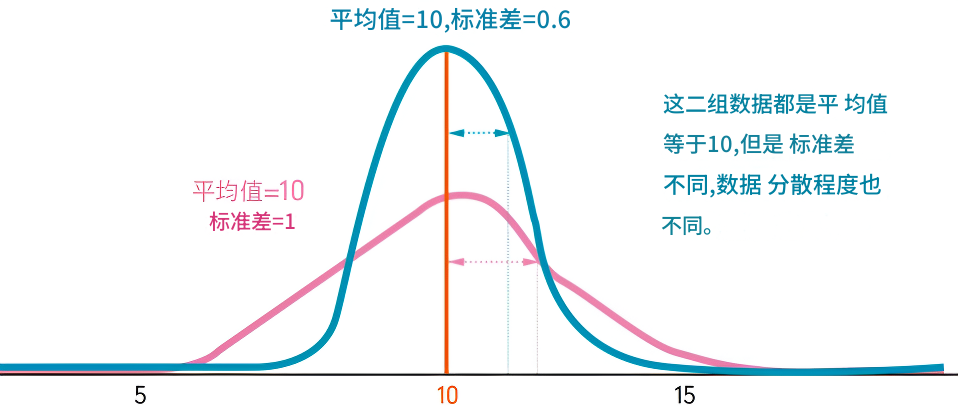
标准差(Standard Deviation, σ)是用来衡量一组数据离散程度的统计学指标，简单来说，它反映了数据点与均值之间的偏离程度。在金融领域，它广泛用于分析资产的波动性、风险评估和投资组合管理。

例如，如果我们有一组学生的考试成绩，它可以告诉我们这些成绩是集中在某个值附近，还是分布得比较广。它越大，意味着数据的波动性越大，价格的波动范围更广。

对于股票、外汇或期货市场来说，如果某只资产的差值较高，就说明它的价格波动较大，投资者可能面临较高的风险。然而，差值大也意味着潜在的回报可能更高。较大的波动可能带来更大的利润空间，因为价格的波动幅度为投资者提供了更多的获利机会。

因此，投资者需要根据自身的风险承受能力来决定是否接受这种波动，并进行相应的投资决策。在投资组合管理中，资产的标准差越大，意味着需要更多的风险控制措施，以平衡风险和回报，确保投资目标的实现。

标准差的优缺点

它是一个很有用的工具，它的优点之一就是简单易懂。通过它，投资者可以快速了解某个资产的波动性，也就是价格的变动幅度。例如，投资者可以通过它来判断一只股票或期货的风险水平，帮助做出决策。

另一个优点是，它广泛适用于各种资产类别。无论是股票、外汇、商品还是期货，它都能帮助投资者分析资产的波动情况。所以它不仅限于某个特定市场，基本上在金融领域的各类资产中都能找到它的身影。

不过，标准差也有它的缺点。首先，它对极端值非常敏感。如果某个资产的价格突然出现异常波动，这个极端值会显著影响它的计算，可能让投资者觉得资产的风险比实际情况要高。换句话说，它在面对剧烈波动时可能无法准确反映出整体的风险水平。

另外，它只是衡量波动的大小，无法告诉我们价格的走势方向。它并不会区分价格是上涨还是下跌，只能告诉我们价格在一定时间内的波动幅度。因此，虽然它能够衡量风险，但它并不能给出关于市场趋势的任何方向性指引，投资者仍然需要结合其他工具和指标来进行全面分析。

标准差在金融中的应用

在金融领域，它常用于衡量资产的波动性。例如，股票、期货或外汇的价格波动较大时，它的差值也较高。这反映了市场的不确定性和波动情况，投资者可以通过它来评估市场的历史波动性。当某个资产的差值较高时，意味着价格波动剧烈，风险也较大。反之，差值较小表示市场波动较小，风险也较低。

在风险管理方面，它帮助投资者评估资产的风险，进而做出更为合理的资产配置。如果资产的差值较高，这表明该资产的风险也较大，可能会带来更大的回报，但也伴随着更多的不确定性。投资者可以通过对比不同资产的差值来优化投资组合，以实现风险与回报的平衡。

它在技术分析中也有广泛应用。布林带就是一个典型的例子。它基于均线，并结合上下两条基于标准差计算的轨道，用来评估市场的超买或超卖情况。当价格触及上轨时，可能意味着市场被过度买入，价格有回调的风险;而当价格触及下轨时，可能意味着市场被过度卖出，价格可能会反弹。

在风险调整后的收益计算中，它同样发挥着重要作用。夏普比率是衡量每单位风险带来回报的常用指标，它通过它来调整投资收益。如果差值较大，意味着风险较高，投资者需要根据这个信息来判断是否能接受这种风险与潜在回报。

此外，它在期权定价中也有重要作用，尤其是在波动率分析中。期权的价格通常会受到市场波动的影响，波动性越大，期权的价值通常越高。因此，它作为衡量波动性的重要工具，直接影响期权的定价。通过这些应用，它在金融市场中帮助投资者更好地理解和管理风险，做出更为精确的决策。

总的来说，标准差是一个简明而有效的工具，它帮助投资者量化和理解市场波动及风险。从股票到期货，再到外汇，它在各类金融资产中都有广泛的应用。尽管它有其局限性，如对极端波动过于敏感，但它依然是衡量风险和波动性的核心指标。